顺序搜索

顺序查找又称为线性查找，是一种最简单的查找方法。适用于线性表的顺序存储结构和链式存储结构。该算法的时间复杂度为O(n)。

从第一个元素m开始逐个与需要查找的元素x进行比较，当比较到元素值相同(即m=x)时返回元素m的下标，如果比较到最后都没有找到，则返回-1。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

# 最基础的遍历无序列表的查找算法
# 时间复杂度O(n)
 
def sequential_search(lis, key):
  length = len(lis)
  for i in range(length):
    if lis[i] == key:
      return i
    else:
      return False
 
if __name__ == '__main__':
  LIST = [1, 5, 8, 123, 22, 54, 7, 99, 300, 222]
  result = sequential_search(LIST, 123)
  print(result)

二分查找

二分查找（Binary Search），是一种在有序数组中查找某一特定元素的查找算法。查找过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则查找过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# 针对有序查找表的二分查找算法
 
def binary_search(lis, key):
  low = 0
  high = len(lis) - 1
  time = 0
  while low < high:
    time += 1
    mid = int((low + high) / 2)
    if key < lis[mid]:
      high = mid - 1
    elif key > lis[mid]:
      low = mid + 1
    else:
      # 打印折半的次数
      print("times: %s" % time)
      return mid
  print("times: %s" % time)
  return False
 
if __name__ == '__main__':
  LIST = [1, 5, 7, 8, 22, 54, 99, 123, 200, 222, 444]
  result = binary_search(LIST, 99)
  print(result)

二叉树

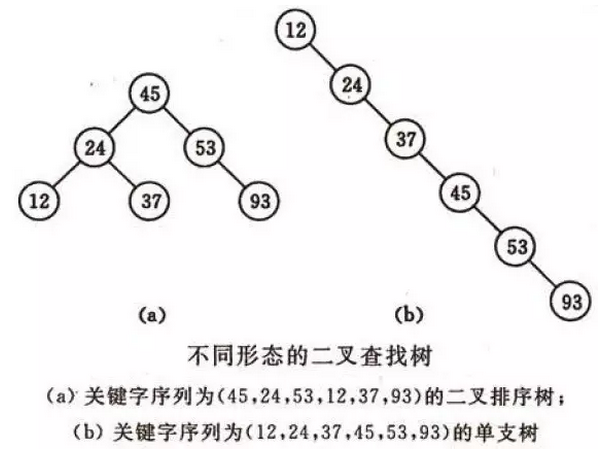
二叉查找树是先对待查找的数据进行生成树，确保树的左分支的值小于右分支的值，然后在就行和每个节点的父节点比较大小，查找最适合的范围。 这个算法的查找效率很高，但是如果使用这种查找方法要首先创建树。

二叉查找树性质：对二叉查找树进行中序遍历，即可得到有序的数列

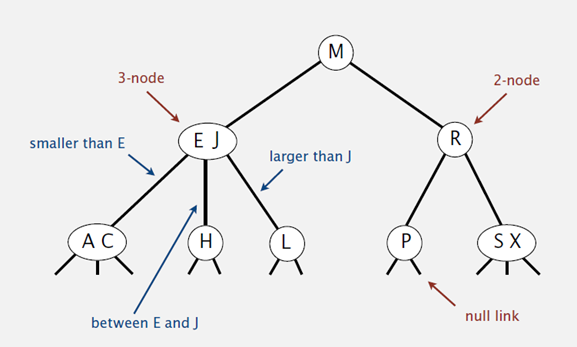
image-20220425100347726

2-3查找树（2-3 Tree）

和二叉树不一样，2-3树运行每个节点保存1个或者两个的值。对于普通的2节点(2-node)，他保存1个key和左右两个自己点。对应3节点(3-node)，保存两个Key，2-3查找树的定义如下： 　　 1）要么为空，要么： 　　 2）对于2节点，该节点保存一个key及对应value，以及两个指向左右节点的节点，左节点也是一个2-3节点，所有的值都比key要小，右节点也是一个2-3节点，所有的值比key要大。 　　 3）对于3节点，该节点保存两个key及对应value，以及三个指向左中右的节点。左节点也是一个2-3节点，所有的值均比两个key中的最小的key还要小；中间节点也是一个2-3节点，中间节点的key值在两个跟节点key值之间；右节点也是一个2-3节点，节点的所有key值比两个key中的最大的key还要大。

image-20220425100347726

平衡二叉树

对二叉排序树加以约束，要求每个结点的左右两个子树的高度差的绝对值不超过1，这样的二叉树称为平衡二叉树，同时要求每个结点的左右子树都是平衡二叉树，这样，就不会因为一边的疯狂增加导致失衡。

失衡情况包括以下四种：

左左失衡：通过右旋进行调整。

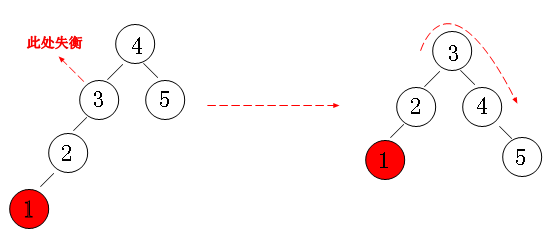
image-20220425100347726

右右失衡：通过左旋进行调整。

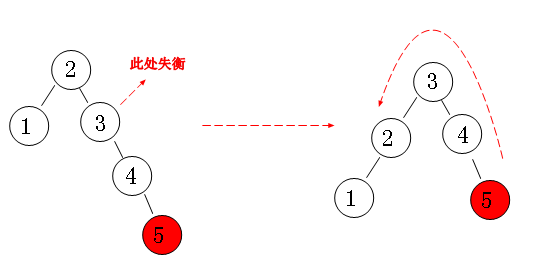
image-20220425100347726

左右失衡：先进行左旋，再进行右旋来调整。

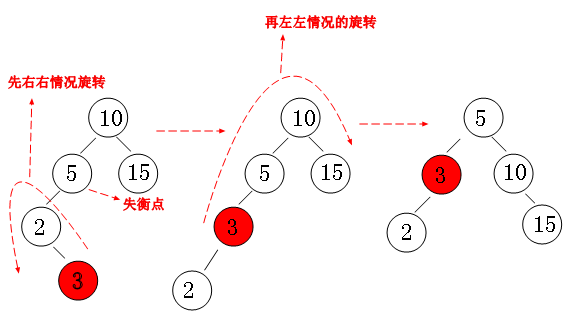
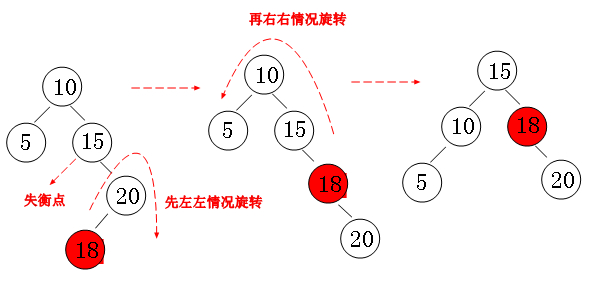
image-20220425100347726

右左失衡：先进行右旋，再进行左旋来调整。

image-20220425100347726

红黑树（Red-Black Tree）

https://blog.csdn.net/weixin_47365232/article/details/124367337

有了平衡二叉树，为什么还需要红黑树？

1、AVL的左右子树高度差不能超过1，每次进行插入、删除操作时，几乎都需要通过旋转操作保持平衡。 2、在频繁进行插入/删除的场景中，频繁的旋转操作使得AVL的性能大打折扣。 3、红黑树通过牺牲严格的平衡，换取插入/删除时少量的旋转操作，整体性能优于AVL。红黑树插入时的不平衡，不超过两次旋转就可以解决；删除时的不平衡，不超过三次旋转就能解决。

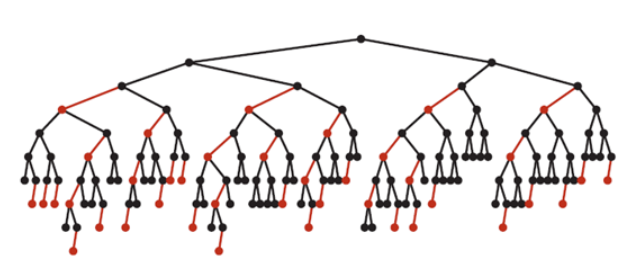
红黑树的特性: （1）每个节点或者是黑色，或者是红色。（非黑即红） （2）根节点是黑色。 （3）每个叶子节点都是黑色的空节点（NIL节点）。 （4）如果一个节点是红色的，则它的子节点必须是黑色的。(根到叶子的所有路径不可能存在两个连续的红色节点) （5）从一个节点到该节点的叶子节点的所有路径上包含相同数目的黑节点。（相同的黑色高度）

约束4和5，保证了红黑树的大致平衡：根到叶子的所有路径中，最长路径不会超过最短路径的2倍。

插入

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

基本的插入规则和平衡二叉树一样，但是在插入后：
1. 将新插入的节点标记为红色。

情况1：父节点是黑色节点，直接插入，无需任何操作调整（不会打破上述规则）

情况2：插入的节点为根结点，则标记为黑色。

情况3：父节点是红色节点，需要调整（打破规则4）。

①叔节点为红色（叔父同色）
	①.1 将叔节点、父节点都标记为黑色
	①.2 祖父节点标记为红色
	①.3 然后把祖父节点当作插入节点进行分析

②叔节点为黑色（叔父异色）

    要分四种情况处理
    a.左左 (父节点是祖父节点的左孩子，并且插入节点是父节点的左孩子)
    进行右旋操作
    b.左右 (父节点是祖父节点的左孩子，并且插入节点是父节点的右孩子)
    进行左旋、再进行右旋操作
    c.右右 (父节点是祖父节点的右孩子，并且插入节点是父节点的右孩子)
    进行左旋操作
    d.右左 (父节点是祖父节点的右孩子，并且插入节点是父节点的左孩子)
    进行右旋、再进行左旋操作
    其实这种情况下处理就和的平衡二叉树一样。

    最后还是对于祖父节点重新进行分析。

image-20220425100347726

B树

B 树可以看作是对2-3查找树的一种扩展，即他允许每个节点有M-1个子节点。 ①根节点至少有两个子节点； ②每个节点有M-1个key，并且以升序排列； ③位于M-1和M key的子节点的值位于M-1 和M key对应的Value之间； ④非叶子结点的关键字个数=指向儿子的指针个数-1； ⑤非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] ； ⑥其它节点至少有M/2个子节点； ⑦所有叶子结点位于同一层； 如：（M=3）

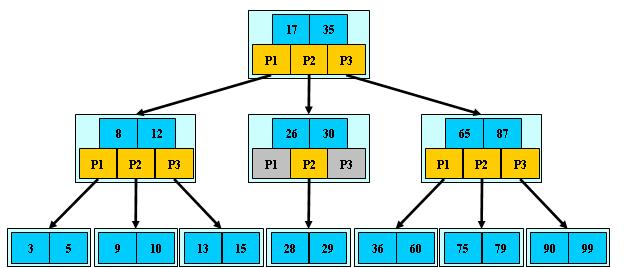
image-20220425100347726

1.关键字集合分布在整颗树中； 2.任何一个关键字出现且只出现在一个结点中； 3.搜索有可能在非叶子结点结束； 4.其搜索性能等价于在关键字全集内做一次二分查找； 5.自动层次控制； 由于限制了除根结点以外的非叶子结点，至少含有M/2个儿子，确保了结点的至少利用率，其最底搜索性能为O(LogN)

B+树

B+树是B-树的变体，也是一种多路搜索树： 1.其定义基本与B-树同，除了： 2.非叶子结点的子树指针与关键字个数相同； 3.非叶子结点的子树指针P[i]，指向关键字值属于[K[i], K[i+1])的子树 4.B-树是开区间； 5.为所有叶子结点增加一个链指针； 6.所有关键字都在叶子结点出现；

如：（M=3）

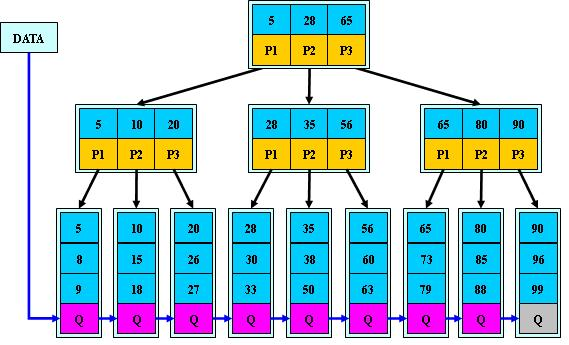
image-20220425100347726

B+树的特性

1.所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的； 2.不可能在非叶子结点命中； 3.非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层； 4.更适合文件索引系统；

文件系统和数据库系统

分块查找

算法简介

要求是顺序表，分块查找又称索引顺序查找，它是顺序查找的一种改进方法。

算法思想

**将n个数据元素"按块有序"划分为m块（m ≤ n）。 ** **每一块中的结点不必有序，但块与块之间必须"按块有序"； ** **即第1块中任一元素的关键字都必须小于第2块中任一元素的关键字； ** 而第2块中任一元素又都必须小于第3块中的任一元素，……

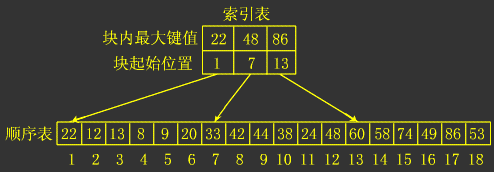
image-20220425100347726

哈希查找

算法简介

哈希表就是一种以键-值(key-indexed) 存储数据的结构，只要输入待查找的值即key，即可查找到其对应的值。

算法思想

哈希的思路很简单，如果所有的键都是整数，那么就可以使用一个简单的无序数组来实现：将键作为索引，值即为其对应的值，这样就可以快速访问任意键的值。这是对于简单的键的情况，我们将其扩展到可以处理更加复杂的类型的键。

算法流程

　　1）用给定的哈希函数构造哈希表； 　　2）根据选择的冲突处理方法解决地址冲突； 　　　　 常见的解决冲突的方法：拉链法和线性探测法。 　　3）在哈希表的基础上执行哈希查找。

倒排索引

搜索引擎对文章进行分词后，再根据关键词建立倒排索引

但是 Lucene 还是一个库，必须要懂一点搜索引擎原理的人才能用的好，所以后来又有人基于 Lucene 进行封装，写出了 Elasticsearch。

https://zhuanlan.zhihu.com/p/62892586?utm_source=qq&utm_medium=social&utm_oi=1204428378759098368